Nonclassical Interferometry
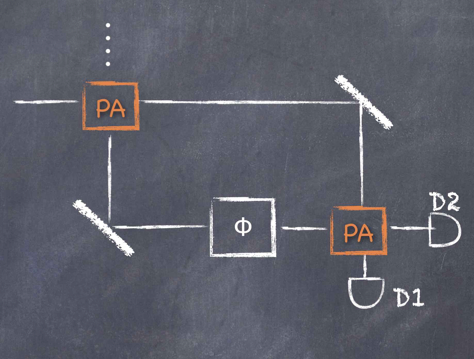
Description
The quest for the fundamental limit of interferometric measurements has been mainly promoted by the international effort aimed to detect gravitational waves by means of long-arm interferometers. In a classical interferometer, where beam-splitters divide and recombine the beams, the shot noise of the coherent states of the input light is responsible for a phase sensitivity limit that scales with the inverse of the square root of the average number of photons at the input, 1/N1/2. In fact, quantum theory of measurement permits to reach a sensitivity that scales much faster, as 1/N (Heisenberg limit). To reach this limit it is necessary to inject genuine quantum states of light in the interferometer. Alternatively, configurations of ‘nonlinear’ interferometers have been proposed, where beam-splitters are replaced with parametric amplifiers. Indeed, a parametric amplifier can be seen as a four-port device which transforms two input states in a couple of strongly correlated amplified output beams. The correlations led to a significant reduction of the final noise, after recombination of the beams on a conventional beam splitter and homodyne detection. In our case, the practical realization of a parametric amplifier is given by an optical parametric oscillator. The initial input states are a classical coherent state in one port and a vacuum state in the other port. In this configuration, we expect the interferometer sensitivity to remarkably surpass the shot noise limit.
INO Staff
Ricciardi Iolanda (Contact Person)
